
時至今日,時頻分析方法至今已經歷了近70年的發展,在這些年的發展過程中,為解決不同的問題,形成了多個分支,演變成了多種形式。但總體來看,目前時頻分析方法可分為三類:一是以能量分布方法為主,這類以Cohen類為代表;二是原子分解方法.主要以Gabor變換、短時傅里葉變換、小波變換為代表;三是針對一些特殊應用場景的其他方法,以Hilbert變換、分數階傅里葉變換等為代表。
1. Cohen類變換方法
以Cohen類為代表的能量分布方法為二次方變換(非線性變換),使得信號的能量沿著瞬時頻率聚集,從而反映出信號能量在時頻平面上的變化關系。這種能量聚集特性很好地保留了信號的邊緣特性、實值性、時移和頻移不變性等,使得其具有較為廣泛的應用。但是這種方法也存在著比較嚴重的缺陷:一是時頻分布的自項之間以及多信號之間會產生交叉項,形成的虛假信號會干擾真實信號的分析;二是二次積分導致運算復雜度過大,當進行大規模特征提取和分析時,或者對信號進行實時分析時,在工程上難以實現。
2.原子類變換方法
原子分解類方法是線性變換,將信號分解成在時間和頻率上都有明確物理意義的時頻點的線性組合,可通過幅度、相位、頻率的變化與時頻點之間的對應關系,利用信號時頻分布進行特征參數估計、調制類型識別、信號解調等。
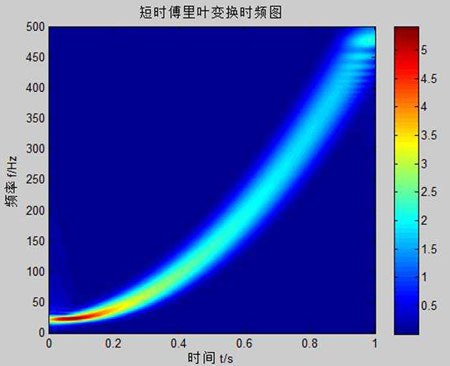
具有代表性的短時傅里葉變換,目前在信號處理領域應用十分廣泛。短時傅里葉的核心思想是:在對信號進行傅里葉變換前,乘上一個有限長的時間窗函數,通過時間窗在時間軸上的逐點移動使信號逐段進人被分析狀態,這樣就得到信號在不同時刻的頻譜特征,得到的信號特征不僅具有頻域信息,也有時域信息,有效地將時域和頻域聯系在了一起。短時傅里葉變換的一個重要特點是:當其窗函數的長度和形狀確定以后,其頻域分辨率也就確定了,這種特點的好處是其時頻系數的幅度隨著頻率的變化具有穩定性,因此在信號處理中被廣泛運用。
另一個具有代表性的方法為小波變換,其核心思想是:通過改變尺度因子大小從而調整小波窗口的大小,當尺度因子變大時,其分析窗口“拉長”,頻率分辨率變高;反之,則頻率分辨率變低。這種能夠自適應調整的時一頻窗,有著“數學顯微鏡”的美稱;目前,小波變換已被廣泛應用于載頻估計、符號率估計、調制類型識別、符號識別、雷達信號脈內特殊調制類型的識別等領域。

掃一掃咨詢微信客服